参考文献:《算法导论(中文第二版)》Thomas H.Cormen, Charles E.Leiserson, Ronald L.Rivest, Clifford Stein [著]、《数据结构(C语言版)》严蔚敏, 吴伟民 [著]
二叉查找树在极端情况下会出现退化的情况,使得查找的时间从对数时间又回到了线性时间,使查找树平衡的想法源自 Adel’son-Vel’skii 和 E.M.Landis,它们在 1962 年发表的论文《An algorithm for the organization of imformation》中提出了一种称为 AVL Tree 的平衡查找树,AVL 树是一种高度平衡的二叉查找树:对每一个结点 x,x 的左子树与右子树的高度差至多为 1,因此一棵有 n 个结点的 AVL 树,其高度为 O(log n)。要实现一棵 AVL 树,需要在每个树结点内维护一个额外的平衡域,该域的值等于该结点左子树的高度减去右子树高度所得的差。
本文涉及的所有代码下载链接为:http://xule.ren/wp-content/uploads/2017/01/AVLTree.zip
AVL 树结点的定义如下,BF 域存储结点左子树与右子树的高度差,称为平衡因子:
/**
* @brief Node type of a balanced binary search tree(AVL tree).
*
* @tparam _Key Type of key objects.
* @tparam _Value Type of mapped objects.
*/
template <typename _Key, typename _Value>
class AVLNode
{
public:
AVLNode() : key(), value(), left(NULL), right(NULL), BF(0) {}
AVLNode(_Key k, _Value v) : key(k), value(v), left(NULL), right(NULL), BF(0) {}
_Key key; ///< key of this node.
_Value value; ///< value of this node.
AVLNode *left; ///< pointing to the left child node of this node.
AVLNode *right; ///< pointing to the right child node of this node.
int BF; ///< balance factor
};
相比于前一篇博文中 BSNode 的定义,由于后面 AVLTree 的实现中未使用到 parent 指针域,因此每个 AVLNode 不包含 parent 指针域。AVL 树的定义如下(该实现也是采用模板泛化的):
#ifndef __AVLTREE_H__
#define __AVLTREE_H__
#include <cstdlib>
#include <vector>
#include <stack>
#include <functional>
#include <cassert>
/**
* @brief A balanced binary search tree(AVL tree), which can be retrieved based on a key, in logarithmic time.
*
* @tparam _Key Type of key objects.
* @tparam _Value Type of mapped objects.
* @tparam _Compare Comparison function object type, defaults to less<_Key>.
*/
template <typename _Key, typename _Value, typename _Compare = std::less<_Key> >
class AVLTree
{
public:
/** @name constructors, destructor of AVLTree. */
///@{
AVLTree() : node_count(0), key_compare(), root(NULL) {}
AVLTree(const _Compare& _compare) : node_count(0), key_compare(), root(NULL) {}
AVLTree(const AVLTree& rhs) : node_count(rhs.node_count), key_compare(rhs.key_compare), root(rhs.root) {}
~AVLTree() { clear(); }
///@}
AVLTree& operator=(const AVLTree& rhs)
{
node_count = rhs.node_count;
key_compare = rhs.key_compare;
root = rhs.root;
return *this;
}
/** @name APIs of AVLTree. */
///@{
/** @brief return true if AVLTree has no nodes. */
bool empty() { return node_count == 0; }
/** @brief return the number of nodes of AVLTree. */
size_t size() { return node_count; }
/** @brief return the left-most node of AVLTree. */
AVLNode<_Key, _Value>* minimum();
/** @brief return the right-most node of AVLTree. */
AVLNode<_Key, _Value>* maximum();
/** @brief return the point to the finding node if found, return NULL if not found. */
AVLNode<_Key, _Value>* find(_Key k);
/**
* @brief insert a node.
*
* @param k key of AVLNode.
* @param v value of AVLNode.
* @return point to the inserted AVLode.
*/
AVLNode<_Key, _Value>* insert(_Key k, _Value v);
/** @brief erase a node only need adjust points. */
void erase(_Key k);
/** @brief erase all the nodes of AVLTree. */
void clear();
///@}
/** @name Traverse methods of AVLTree. */
///@{
void preOrderTraverse(std::vector<AVLNode<_Key, _Value>* >& vec);
void inOrderTraverse(std::vector<AVLNode<_Key, _Value>* >& vec);
void postOrderTraverse(std::vector<AVLNode<_Key, _Value>* >& vec);
///@}
private:
/** @name Critical methods of AVLTree. */
///@{
/** @brief insert a node(recursively). */
bool _insert(AVLNode<_Key, _Value> **p, AVLNode<_Key, _Value> *node, bool& taller);
/** @brief erase a node(recursively). */
bool _erase(AVLNode<_Key, _Value> **p, _Key& k, bool& taller);
/** @brief erase a node which has both left and right children(recursively). */
void _erase(AVLNode<_Key, _Value> *q, AVLNode<_Key, _Value> **r, bool& taller);
/** @brief rebalance left subtree of the erased node. */
void leftRebalance(AVLNode<_Key, _Value> **p, bool& taller);
/** @brief rebalance right subtree of the erased node. */
void rightRebalance(AVLNode<_Key, _Value> **p, bool& taller);
/** @brief execute LL rotate as to node p. */
AVLNode<_Key, _Value>* rotateLL(AVLNode<_Key, _Value> **p);
/** @brief execute RR rotate as to node p. */
AVLNode<_Key, _Value>* rotateRR(AVLNode<_Key, _Value> **p);
/** @brief execute LR rotate as to node p. */
AVLNode<_Key, _Value>* rotateLR(AVLNode<_Key, _Value> **p);
/** @brief execute RL rotate as to node p. */
AVLNode<_Key, _Value>* rotateRL(AVLNode<_Key, _Value> **p);
///@}
private:
size_t node_count; ///< maintaining the number of nodes of AVLTree.
_Compare key_compare; ///< key compare predicate of AVLNode.
AVLNode<_Key, _Value> *root; ///< root node of AVLTree.
};
#endif /* __AVLTREE_H__ */
minimum()、maximum()、find()、clear() 函数及三种遍历方法的实现与 BSTree 并无差异,在此不再赘述,AVL 树的关键在于插入操作和删除操作,其中插入操作稍微简单一些,由于插入和删除操作都必须修改树结点的平衡因子,都有可能破坏树的平衡性,根据破坏情况的不同,主要分为四类情况,而重新恢复平衡性需要对树中的失衡子树部分做旋转操作,要恢复四类被破坏的情况,分别需要作四类旋转:LL、RR、LR、RL,下面逐一介绍。
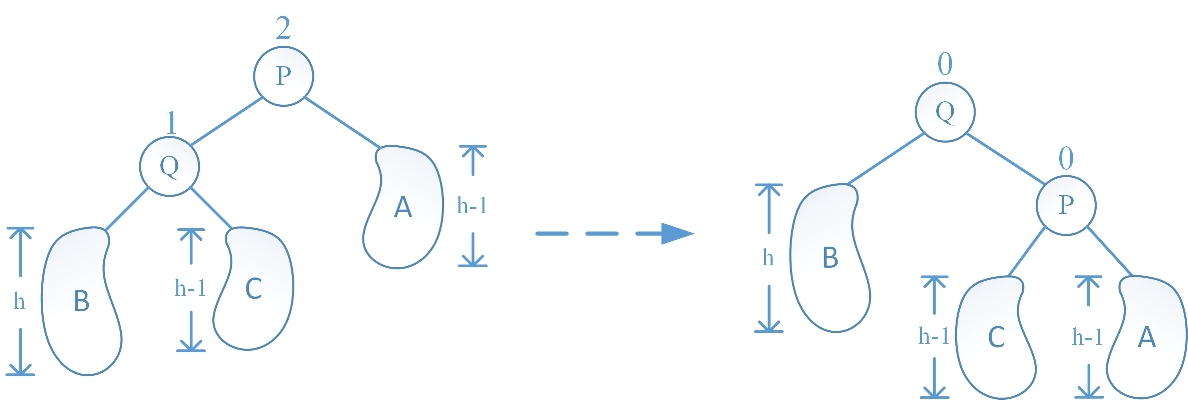
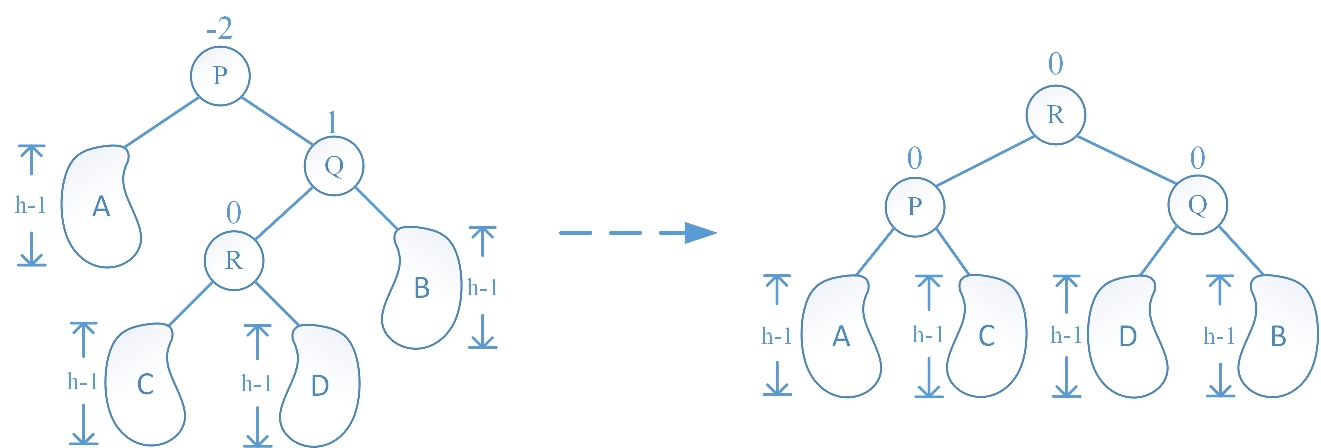
情况一、LL 旋转
根据图示,在 Q 结点的左子树 B 中插入了一个新结点后,使得 B 的高度从 h-1 增加到了 h,从而使得 Q 结点的平衡因子从 0 变成 1,而 Q 结点的父节点 P 的平衡因子从 1 变成了 2,出现了失衡情况,采用 LL 旋转可重新恢复树的平衡性:让 Q 的右子树成为 P 的左子树,再让 Q 的右孩子指针指向 P,最后更新下 P、Q 结点平衡因子即可,代码如下:
template <typename _Key, typename _Value, typename _Compare>
AVLNode<_Key, _Value>* AVLTree<_Key, _Value, _Compare>::rotateLL(AVLNode<_Key, _Value> **p)
{
AVLNode<_Key, _Value> *q = (*p)->left;
(*p)->left = q->right;
q->right = *p;
(*p)->BF = q->BF = 0;
return q;
}
函数返回旋转后新子树的根结点,是为了在后面插入函数的递归实现中能够更新原失衡子树的根结点的父结点的孩子指针,后面的 rotateRR、rotateLR、rotateRL 函数返回的意义与此相同。
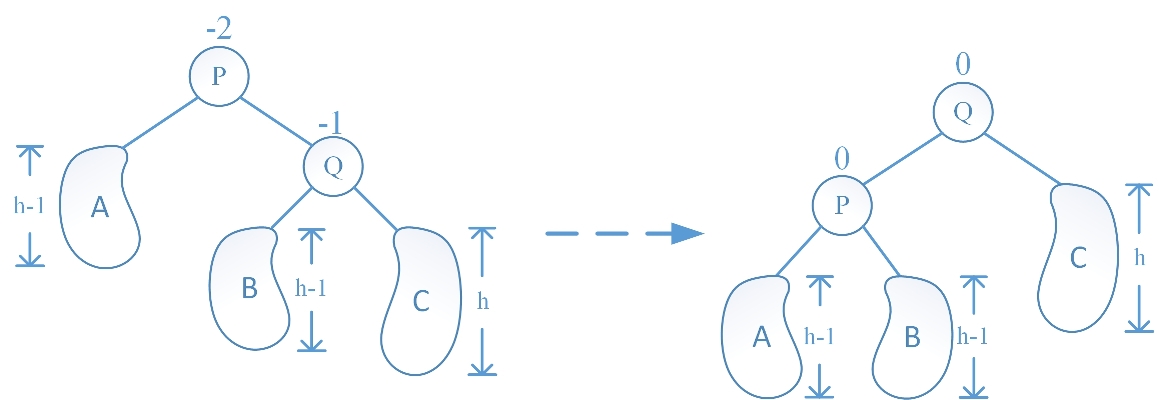
情况二、RR 旋转
根据图示,在 Q 结点的右子树 C 中插入了一个新结点后,使得 C 的高度从 h-1 增加到了 h,从而使得 Q 结点的平衡因子从 0 变成 -1,而 Q 结点的父节点 P 的平衡因子从 -1 变成了 -2,出现了失衡情况,采用 RR 旋转可重新恢复树的平衡性:让 Q 的左子树成为 P 的右子树,再让 Q 的左孩子指针指向 P,最后更新下 P、Q 结点平衡因子即可,代码如下:
template <typename _Key, typename _Value, typename _Compare>
AVLNode<_Key, _Value>* AVLTree<_Key, _Value, _Compare>::rotateRR(AVLNode<_Key, _Value> **p)
{
AVLNode<_Key, _Value> *q = (*p)->right;
(*p)->right = q->left;
q->left = *p;
(*p)->BF = q->BF = 0;
return q;
}
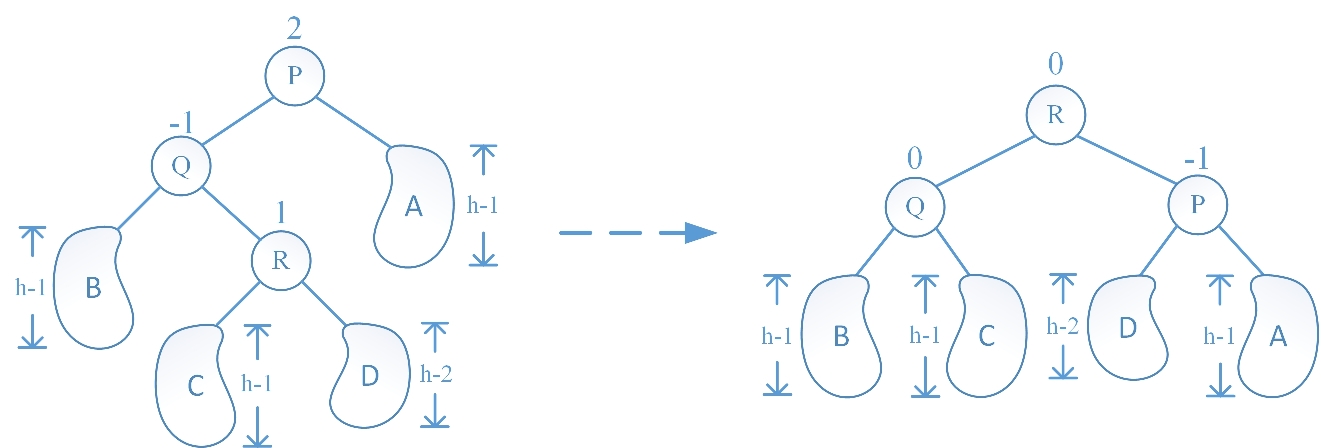
情况三、LR 旋转
LR 旋转的情况与 LL 旋转的情况的不同在于:在 LL 中是由于 Q 结点的左子树增高破坏子树的平衡性,而在 LR 中是由于 Q 结点的右子树增高破坏子树的平衡性。LR 旋转操作过程为:先让 R 结点的左子树成为 Q 结点的右子树,再让 R 结点的左孩子指针指向 Q 结点,随后让 R 结点的右子树成为 P 结点的左子树,做让 R 结点的右孩子指针指向 P 结点,最后更新 P、Q、R 结点的平衡因子时又根据旋转前 R 结点的平衡因子分为三种情况(插入新结点后 R 结点的左右子树高度相等、R 结点的左子树高于右子树、R 结点的右子树高于左子树),分别绘图如下:
Case I:R 结点的左右子树高度相等:
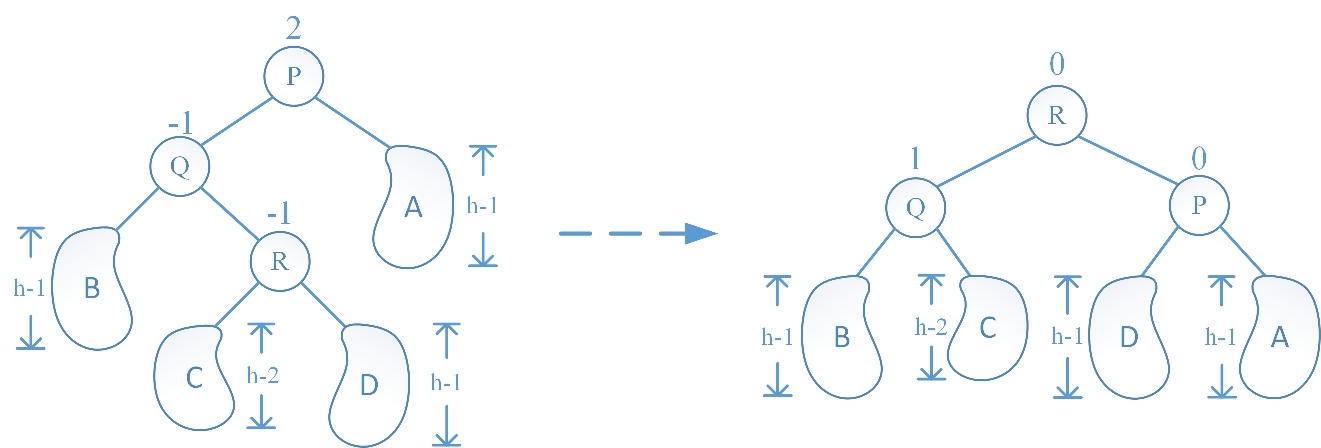
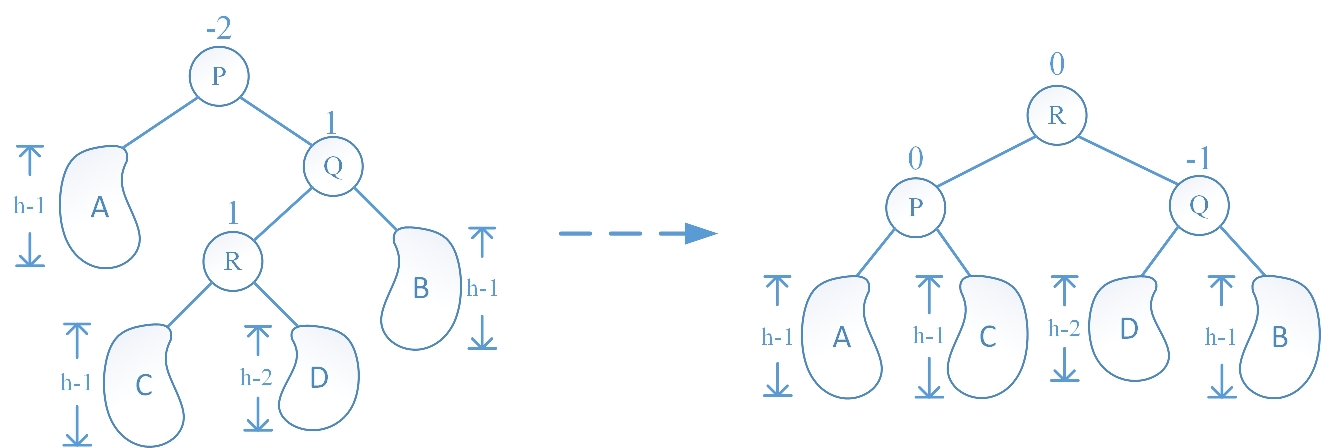
Case II:R 结点的左子树高于右子树:
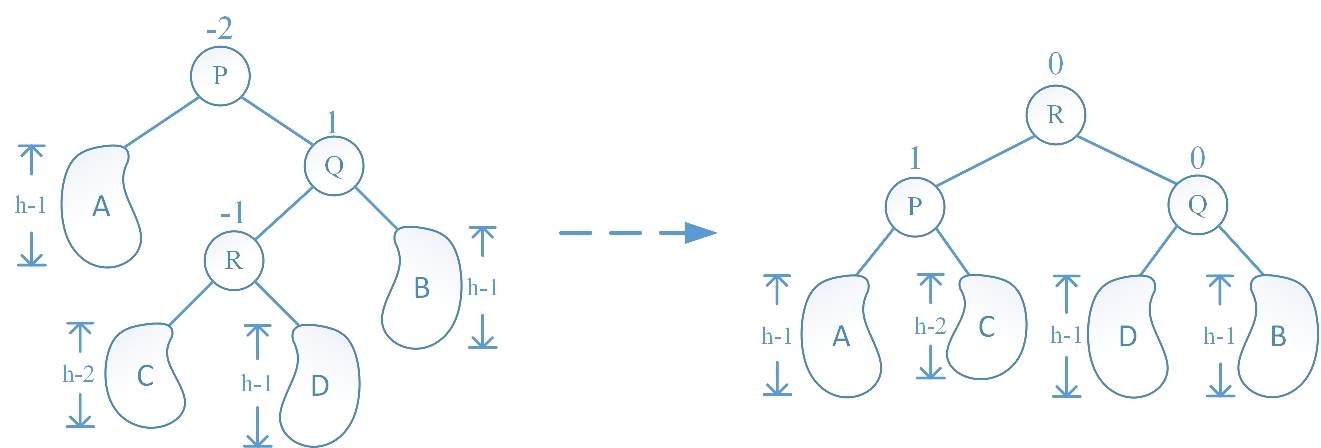
Case III:R 结点的右子树高于左子树:
LR 旋转函数代码如下:
template <typename _Key, typename _Value, typename _Compare>
AVLNode<_Key, _Value>* AVLTree<_Key, _Value, _Compare>::rotateLR(AVLNode<_Key, _Value> **p)
{
AVLNode<_Key, _Value> *q = (*p)->left;
assert( (*p)->BF == 2 && q->BF == -1 );
int flag = q->right->BF; // q->right->BF == { 1, -1, 0 }
(*p)->left = rotateRR(&q);
q->BF = flag == 1 ? 0 : (flag == -1 ? 1 : 0);
AVLNode<_Key, _Value> *r = rotateLL(p); // r->BF == 0 always true
(*p)->BF = flag == 1 ? -1 : (flag == -1 ? 0 : 0);
return r;
}
情况四、RL 旋转
RL 旋转的情况与 RR 旋转的情况的不同在于:在 RR 中是由于 Q 结点的右子树增高破坏子树的平衡性,而在 RL 中是由于 Q 结点的左子树增高破坏子树的平衡性。RL 旋转操作过程为:先让 R 结点的右子树成为 Q 结点的左子树,再让 R 结点的右孩子指针指向 Q 结点,随后让 R 结点的左子树成为 P 结点的右子树,做让 R 结点的左孩子指针指向 P 结点,最后更新 P、Q、R 结点的平衡因子时又根据旋转前 R 结点的平衡因子也分为三种情况(插入新结点后 R 结点的左右子树高度相等、R 结点的左子树高于右子树、R 结点的右子树高于左子树),分别绘图如下:
Case I:R 结点的左右子树高度相等:
Case II:R 结点的左子树高于右子树:
Case III:R 结点的右子树高于左子树:
RL 旋转函数代码如下:
template <typename _Key, typename _Value, typename _Compare>
AVLNode<_Key, _Value>* AVLTree<_Key, _Value, _Compare>::rotateRL(AVLNode<_Key, _Value> **p)
{
AVLNode<_Key, _Value> *q = (*p)->right;
assert( (*p)->BF == -2 && q->BF == 1 );
int flag = q->left->BF; // q->left->BF == { 1, -1, 0 }
(*p)->right = rotateLL(&q);
q->BF = flag == 1 ? -1 : (flag == -1 ? 0 : 0);
AVLNode<_Key, _Value> *r = rotateRR(p); // r->BF == 0 always true
(*p)->BF = flag == 1 ? 0 : (flag == -1 ? 1 : 0);
return r;
}
insert
了解完上述四种旋转方式后,下面来看 AVL 树的插入操作,API 函数 insert() 代码如下:
template <typename _Key, typename _Value, typename _Compare>
AVLNode<_Key, _Value>* AVLTree<_Key, _Value, _Compare>::insert(_Key k, _Value v)
{
AVLNode<_Key, _Value>* node = new AVLNode<_Key, _Value>(k, v);
bool taller = false;
bool hasInsert = _insert(&root, node, taller);
if (hasInsert)
++node_count;
return hasInsert ? node : NULL;
}
在函数 insert() 中,首先根据传入的参数创建新结点,随后定义布尔变量 taller 用于指示子树是否有高度变化,在 _insert() 函数的递归回溯过程中就是根据 taller 决定是否要进行平衡因子的更新操作,_insert() 函数返回一个布尔值,表示是否已经将该新创建结点插入了 AVL 树中,只有当原先 AVL 树中存在某个结点其关键字 key 与函数 insert() 的传入参数 k 相等的情况,也就是原先树中已经包含该关键字的结点时,_insert() 函数会返回 false 并且将新创建的结点 delete,若已插入,函数 insert() 返回指向该新插入结点的指针供调用代码使用;若未插入,函数 insert() 返回 NULL 通知调用代码树中已经存在该键值结点。内部实现函数 _insert() 的代码如下:
template <typename _Key, typename _Value, typename _Compare>
bool AVLTree<_Key, _Value, _Compare>::_insert(AVLNode<_Key, _Value> **p, AVLNode<_Key, _Value> *node, bool& taller)
{
if ((*p) == NULL)
{
(*p) = node;
taller = true;
return true;
}
if (key_compare(node->key, (*p)->key)) // node->key < p->key
{
if (_insert(&((*p)->left), node, taller) == false)
return false;
if (taller)
{
switch ((*p)->BF)
{
case 1:
{
(*p)->BF = 2;
if ((*p)->left->BF == 1)
*p = rotateLL(p);
else // p->left->BF == -1
*p = rotateLR(p);
taller = false;
break;
}
case 0:
{
(*p)->BF = 1;
taller = true;
break;
}
case -1:
{
(*p)->BF = 0;
taller = false;
break;
}
}
}
}
else if (key_compare((*p)->key, node->key)) // node->key > p->key
{
if (_insert(&((*p)->right), node, taller) == false)
return false;
if (taller)
{
switch ((*p)->BF)
{
case 1:
{
(*p)->BF = 0;
taller = false;
break;
}
case 0:
{
(*p)->BF = -1;
taller = true;
break;
}
case -1:
{
(*p)->BF = -2;
if ((*p)->right->BF == -1)
*p = rotateRR(p);
else // p->right->BF == 1
*p = rotateRL(p);
taller = false;
break;
}
}
}
}
else // node->key == p->key
{
delete node;
taller = false;
return false;
}
return true;
}
该函数是递归的,每次进入的 p 都是不同的,根据新创建结点 node 的关键字大小,不断地从根结点往叶子结点方向深入查找新创建结点的合适插入位置,找到该合适位置后,将 node 赋给 *p,同时置 taller 为 true 指示刚刚从根结点深入到该位置的这条路径上的各结点的平衡因子都可能需要被更新,这最里面一层的 *p 就是外面那层的 (*p)->left 或是 (*p)->right,也就是将插入位置的父结点的某个孩子指针(取决于键值)指向新结点,在递归的返回过程中,从刚刚从根结点深入的那条路径反向回溯,根据 taller 对沿途的结点作平衡因子的更新,若发现破坏树的平衡性了,则针对具体的那四种情况作相应的旋转调整,注意到旋转调整之后的 taller 被置为 false,这表明一棵有 n 个结点的 AVL 树,其插入操作执行 O(1) 次旋转,此外对于已经存在该键值结点的情况,delete 掉新创建的结点防止内存泄漏,同时置 taller 为 false 并返回 false,因为此时树没有任何变化。
erase
下面来看 AVL 树的删除操作,API 函数 erase() 代码如下,与 insert() 函数一样,真正的实现交由 _erase() 函数完成:
template <typename _Key, typename _Value, typename _Compare>
void AVLTree<_Key, _Value, _Compare>::erase(_Key k)
{
bool taller = false;
bool hasErase = _erase(&root, k, taller);
if (hasErase)
--node_count;
}
函数 _erase() 仅在真正删除了树结点的时候返回 true,若树中不存在传入参数 k 为键值的结点,则 _erase() 返回 false。内部实现函数 _erase() 的代码如下:
#define REPLACED_BY_PREDECESSOR_IN_ERASE 1
template <typename _Key, typename _Value, typename _Compare>
bool AVLTree<_Key, _Value, _Compare>::_erase(AVLNode<_Key, _Value> **p, _Key& k, bool& taller)
{
if (*p == NULL)
return false;
if (key_compare(k, (*p)->key)) // k < p->key
{
if (_erase(&((*p)->left), k, taller) == false)
return false;
if (taller)
leftRebalance(p, taller);
}
else if (key_compare((*p)->key, k)) // k > p->key
{
if (_erase(&((*p)->right), k, taller) == false)
return false;
if (taller)
rightRebalance(p, taller);
}
else // k == p->key
{
AVLNode<_Key, _Value> *q = *p;
if ((*p)->left == NULL)
{
(*p) = (*p)->right;
delete q;
taller = true;
}
else if ((*p)->right == NULL)
{
(*p) = (*p)->left;
delete q;
taller = true;
}
else // (*p)->left != NULL && (*p)->right != NULL
{
#if REPLACED_BY_PREDECESSOR_IN_ERASE
_erase(q, &q->left, taller);
if (taller)
leftRebalance(&q, taller);
#else
_erase(q, &q->right, taller);
if (taller)
rightRebalance(&q, taller);
#endif
*p = q;
}
}
return true;
}
与插入操作的思路一致,先是从根结点开始逐渐深入找到要删除的结点所在位置,若没有找到,则函数入口处的 if (*p == NULL) 成立,函数逐层返回 false;若找到,先判断待删除结点子树的个数,若其只有一棵子树,直接在调整待删除结点父结点的孩子指针后直接删除该结点即可,同时置 taller 为 true,以便在递归的返回过程中不断地更新该删除结点所有祖先结点的平衡因子,这里将平衡因子调整部分代码抽离出来写成了函数 leftRebalance() 和 rightRebalance(),若删除结点原先在其某个祖先结点的右子树中,则递归返回到该祖先结点时若 taller 仍为 true,则调用 leftRebalance(),若删除结点原先在其某个祖先结点的左子树中,则调用 rightRebalance();若待删除结点左右子树都不为空,则存在两种删除方案,即二叉查找树中采用待删除结点的前趋还是后继的内容来替代待删除结点的内容随后再删除该前趋或后继,代码中使用宏 REPLACED_BY_PREDECESSOR_IN_ERASE 来区分两种实现的代码,这里以使用前趋结点替代为例叙述代码思路:由于前驱结点必定在左子树当中,首先对 q 的左孩子调用 _erase() 函数的重载版本,随后根据 taller 来决定是否需要进行 leftRebalance(),最后注意修改 *p,赋值给 *p 的 q 仅有可能在 leftRebalance() 中被修改,因为 _erase() 函数的重载版本对 q 进行的是值传递,该重载版本完整代码如下:
template <typename _Key, typename _Value, typename _Compare>
void AVLTree<_Key, _Value, _Compare>::_erase(AVLNode<_Key, _Value> *q, AVLNode<_Key, _Value> **r, bool& taller)
{
#if REPLACED_BY_PREDECESSOR_IN_ERASE
if ((*r)->right == NULL) // r is the predecessor of the erased node q
{
q->key = (*r)->key;
q->value = (*r)->value;
q = *r; // pointer q is passed by value, needn't worry about modifying it
*r = (*r)->left; // make (*r)->parent->right = (*r)->left
delete q;
taller = true; // after erasing the predecessor of node q, height decreased by 1
}
else
{
_erase(q, &(*r)->right, taller); // equivalent to always execute *r = (*r)->right, indicating to find the right-most node in the left-subtree of q
if (taller)
rightRebalance(r, taller);
}
#else
if ((*r)->left == NULL) // r is the successor of the erased node q
{
q->key = (*r)->key;
q->value = (*r)->value;
q = *r; // pointer q is passed by value, needn't worry about modifying it
*r = (*r)->right; // make (*r)->parent->left = (*r)->right
delete q;
taller = true; // after erasing the successor of node q, height decreased by 1
}
else
{
_erase(q, &(*r)->left, taller); // equivalent to always execute *r = (*r)->left, indicating to find the left-most node in the right-subtree of q
if (taller)
leftRebalance(r, taller);
}
#endif
}
首先递归调用该重载版本,找到待删除结点的前趋结点,找到后删除该前趋结点并调整好该前趋结点父结点的孩子指针域,随后置 taller 为 true,在递归返回过程中,不断检测 taller 的值决定是否需要进行 rightRebalance(),可以看到采用后继结点替代方式的代码是对偶的。
来看扮演重头戏的函数 leftRebalance() 和 rightRebalance(),前者的代码如下:
template <typename _Key, typename _Value, typename _Compare>
void AVLTree<_Key, _Value, _Compare>::leftRebalance(AVLNode<_Key, _Value> **p, bool& taller)
{
switch ((*p)->BF)
{
case 1:
{
(*p)->BF = 0;
taller = true;
break;
}
case 0:
{
(*p)->BF = -1;
taller = false;
break;
}
case -1:
{
(*p)->BF = -2; // here need a rotate operation to rebalance since the node become unbalanced
AVLNode<_Key, _Value> *q = (*p)->right;
if (q->BF == 0) // operation is similer with RR rotate, but balance factors aren't the same as those after RR rotate
{
(*p)->right = q->left;
q->left = *p;
(*p)->BF = -1;
q->BF = 1;
*p = q;
taller = false;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P Q
* / \ \ / \
* E Q -> Q -> P R
* / \ / \ \
* L R L R L
* height of this subtree didn't change, thus taller is false.
*/
}
else if (q->BF == -1)
{
*p = rotateRR(p);
taller = true;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P Q
* / \ \ / \
* E Q -> Q -> P R
* \ \
* R R
* height of this subtree changed from 3 to 2, thus taller is true.
*/
}
else // (q->BF == 1)
{
*p = rotateRL(p);
taller = true;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P L
* / \ \ / \
* E Q -> Q -> P Q
* / /
* L L
* height of this subtree changed from 3 to 2, thus taller is true.
*/
}
break;
}
default:
assert( false );
}
}
先判断 *p 的平衡因子,若 (*p)->BF == -1,则需要进行旋转,采用的旋转方式则取决于 (*p)->right->BF,旋转后 taller 是否需要置 true 代码中的注释直观明了,需要注意的是画出的 E、Q、L、R 都是可能有子树的,其中删除在结点在子树 E 当中,这里为了简明起见,用结点来表示子树。
rightRebalance() 的代码与此对偶,不再赘述,粘贴如下:
template <typename _Key, typename _Value, typename _Compare>
void AVLTree<_Key, _Value, _Compare>::rightRebalance(AVLNode<_Key, _Value> **p, bool& taller)
{
switch ((*p)->BF)
{
case -1:
{
(*p)->BF = 0;
taller = true;
break;
}
case 0:
{
(*p)->BF = 1;
taller = false;
break;
}
case 1:
{
(*p)->BF = 2; // here need a rotate operation to rebalance since the node become unbalanced
AVLNode<_Key, _Value> *q = (*p)->left;
if (q->BF == 0) // operation is similer with LL rotate, but balance factors aren't the same as those after LL rotate
{
(*p)->left = q->right;
q->right = *p;
(*p)->BF = 1;
q->BF = -1;
*p = q;
taller = false;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P Q
* / \ / / \
* Q E -> Q -> L P
* / \ / \ /
* L R L R R
* height of this subtree didn't change, thus taller is false.
*/
}
else if (q->BF == 1)
{
*p = rotateLL(p);
taller = true;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P Q
* / \ / / \
* Q E -> Q -> L P
* / /
* L L
* height of this subtree changed from 3 to 2, thus taller is true.
*/
}
else // (q->BF == -1)
{
*p = rotateLR(p);
taller = true;
/*
* E is the node to be erased, first step is erase, second step is rotate.
* P P R
* / \ / / \
* Q E -> Q -> Q P
* \ \
* R R
* height of this subtree changed from 3 to 2, thus taller is true.
*/
}
break;
}
default:
assert( false );
}
}
test
对插入及删除操作的完整测试代码如下:
#include "AVLTree.h"
#include <iostream>
using std::cout;
using std::endl;
template <typename _Key, typename _Value>
void printTraverseResult(std::vector<AVLNode<_Key, _Value>* >& v)
{
for (size_t i = 0; i < v.size(); ++i)
cout << v[i]->key << ' ';
cout << endl;
}
template <typename _Key, typename _Value>
void printBalanceFactor(std::vector<AVLNode<_Key, _Value>* >& v)
{
for (size_t i = 0; i < v.size(); ++i)
cout << v[i]->BF << ' ';
cout << endl;
}
void fillAVLTree(AVLTree<int, double>& avlTree)
{
avlTree.insert(1, 3.23);
avlTree.insert(2, 1.34);
avlTree.insert(3, 8.36);
avlTree.insert(4, 9.73);
avlTree.insert(5, 7.18);
avlTree.insert(6, 7.51);
avlTree.insert(7, 8.13);
avlTree.insert(16, 4.16);
avlTree.insert(15, 2.86);
avlTree.insert(14, 1.01);
avlTree.insert(13, 5.69);
avlTree.insert(12, 4.97);
avlTree.insert(11, 9.61);
avlTree.insert(10, 3.27);
avlTree.insert(8, 7.12);
avlTree.insert(9, 8.69);
/*
* After fill, the structure of AVL tree looks:
* 7
*
* / \
*
* 4 13
* / \ / \
* 2 6 11 15
* / \ / / \ / \
* 1 3 5 9 12 14 16
* / \
* 8 10
*/
}
int main(int argc, char *argv[])
{
cout << "Test AVLTree methods: " << endl;
AVLTree<int, double> avlTree;
fillAVLTree(avlTree);
cout << "before erase :\n";
std::vector<AVLNode<int, double>* > preOrderAVL, inOrderAVL, postOrderAVL;
avlTree.preOrderTraverse(preOrderAVL);
avlTree.inOrderTraverse(inOrderAVL);
avlTree.postOrderTraverse(postOrderAVL);
cout << "PreOrder: "; printTraverseResult(preOrderAVL);
cout << "InOrder: "; printTraverseResult(inOrderAVL);
cout << "BalanceFactor: "; printBalanceFactor(inOrderAVL);
cout << "PostOrder: "; printTraverseResult(postOrderAVL);
preOrderAVL.clear(); inOrderAVL.clear(); postOrderAVL.clear();
avlTree.erase(13);
/*
* After erase 13, the structure of AVL tree looks:
* 7
*
* / \
*
* 4 12
* / \ / \
* 2 6 9 15
* / \ / / \ / \
* 1 3 5 8 11 14 16
* /
* 10
*/
cout << "after erase :\n";
avlTree.preOrderTraverse(preOrderAVL);
avlTree.inOrderTraverse(inOrderAVL);
avlTree.postOrderTraverse(postOrderAVL);
cout << "PreOrder: "; printTraverseResult(preOrderAVL);
cout << "InOrder: "; printTraverseResult(inOrderAVL);
cout << "BalanceFactor: "; printBalanceFactor(inOrderAVL);
cout << "PostOrder: "; printTraverseResult(postOrderAVL);
avlTree.clear();
return 0;
}
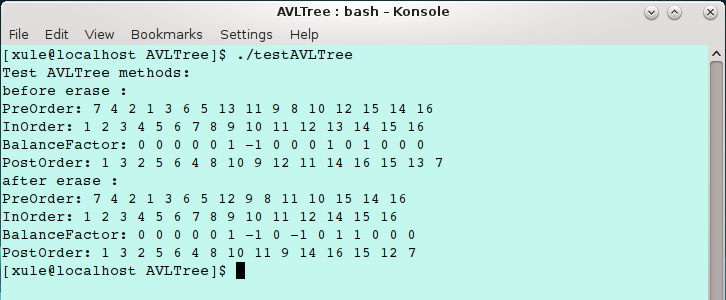
测试程序运行结果如下(其中输出的平衡因子对应于中序遍历,可以看出遍历输出结果与代码中注释的树结构是一致的):
二叉平衡树还有很多类型,比较著名的有 R.Bayer 于 1972 年在论文《Symmetric binary B-trees: Data structure and maintenance algorithms》中提出的红黑树,以及 Daniel D.Sleator 和 Robert E. Tarjan 于 1985 年在论文《Self-adjusting binary search trees》提出的伸展树,此外 William Pugh 于 1990 年在论文《Skip lists: A probabilistic alternative to balanced trees》中提出了跳表这种数据结构,跳表是扩充了一些额外指针域的链表,在一个包含 n 个元素的跳表上,每一种字典操作都在 O(log n) 期望时间内执行,通常情况下,跳表的时间效率比平衡树更好。
nonstd::map
std::map 是通过红黑树来实现的,AVL 树也能作为关联容器 map 的一种实现方式,其定义如下:
#include "AVLTree.h"
namespace nonstd
{
/**
* @brief A non-standard map made up of (key,value) pairs, which can be retrieved based on a key, in logarithmic time.
*
* @tparam _K Type of key objects.
* @tparam _V Type of mapped objects.
* @tparam _C Comparison function object type, defaults to less<_K>.
*/
template <typename _K, typename _V, typename _C = std::less<_K> >
class map
{
public:
/** @name container typedefs for easy of use. */
///@{
typedef _K key_type;
typedef _V data_type;
typedef _V mapped_type;
typedef std::pair<const _K, _V> value_type;
typedef _C key_compare;
typedef AVLNode<_K, _V>* iterator;
///@}
/** @name constructors, destructor of nonstd::map. */
///@{
map() : _M_t() {}
explicit map(const _C& __comp) : _M_t(__comp) {}
map(const map& __x) : _M_t(__x._M_t) { }
~map() { clear(); }
///@}
map& operator=(const map& __x) { _M_t = __x._M_t; return *this; }
/** @name APIs of nonstd::map. */
///@{
bool empty() { return _M_t.empty(); }
size_t size() { return _M_t.size(); }
iterator begin() { return _M_t.minimum(); }
iterator end() { return NULL; }
iterator find(const key_type& __x) { return _M_t.find(__x); }
size_t count(const key_type& __x) { return _M_t.find(__x) == end() ? 0 : 1; }
iterator insert(const value_type& __x) { return _M_t.insert(__x.first, __x.second); }
void erase(const key_type& __x) { _M_t.erase(__x); }
void clear() { _M_t.clear(); }
///@}
private:
AVLTree<_K, _V, _C> _M_t; ///< AVL tree representing nonstd::map.
};
} // end namespace nonstd
nonstd::map 无非就是对 AVL 树包装了一下,该实现相比 std::map 而言要简陋许多,不支持使用迭代器进行迭代访问,不同之处还在于 end() 函数返回一个 NULL 值,而 std::map 的 end() 是返回一个哨兵结点。对 std::map 和 nonstd::map 的性能对比测试完整代码如下:
#include "AVLTree.h"
#include <time.h>
#include <iostream>
#include <map>
#include <algorithm> // random_shuffle
using std::cout;
using std::endl;
/**
* @brief convenience class, which prints procedure executing time between Timer's construction and its destruction.
*/
class Timer
{
public:
/** record constructing time in the constructor. */
explicit Timer(const char *s) : _note(s) { _start_time = clock(); }
~Timer() { cout << _note << elapsed() << "s." << endl; }
/** calculate how much time elapsed since constructed. */
inline double elapsed() { return static_cast<double>(clock() - _start_time) / CLOCKS_PER_SEC; }
private:
Timer(const Timer&);
Timer& operator=(const Timer&);
private:
std::string _note; ///< this string will be printed when timer elapsed.
clock_t _start_time; ///< record the time when the timer is constructed.
};
#define DATA_SCALE 1000000
#define FAIL_RATIO 0.25
inline double dblrand() { return static_cast<double>(rand())/RAND_MAX + (static_cast<double>(rand())/RAND_MAX * (1.0/RAND_MAX)); }
inline int idxrand(int minIdx, int maxIdx) { return rand() % (maxIdx - minIdx) + minIdx; }
int main(int argc, char *argv[])
{
cout << "performance evaluation of AVLTree, compared with std::map which implemented by red-black tree.\n";
std::map<int, double> std_map;
nonstd::map<int, double> nonstd_map;
srand(time(NULL));
int i = 0;
/* generate random keys and values */
std::vector<int> keys;
std::vector<double> values;
keys.reserve(DATA_SCALE);
values.reserve(DATA_SCALE);
for (i = 0; i < DATA_SCALE; ++i)
{
keys.push_back(rand());
values.push_back(dblrand());
}
/* determine the order of elements' index in the operations of insert(), erase() and find() */
std::vector<int> insertOrder, eraseOrder, findOrder;
insertOrder.reserve(2*DATA_SCALE);
eraseOrder.reserve(DATA_SCALE);
findOrder.reserve(DATA_SCALE);
for (i = 0; i < DATA_SCALE; ++i) // 0-100%
{
insertOrder.push_back(i); // 100%
if (i % 4 == 0)
eraseOrder.push_back(i); // 25%
else if (i % 4 == 1)
findOrder.push_back(i); // 25%
}
for (i = 0; i < FAIL_RATIO*DATA_SCALE; ++i)
{
int idx = idxrand(0, DATA_SCALE);
insertOrder.push_back(idx); // FAIL_RATIO * 100%
}
for (i = 0; i < FAIL_RATIO*DATA_SCALE; i += 2)
{
int idx = idxrand(0, DATA_SCALE);
while (idx % 4 < 2)
idx = idxrand(0, DATA_SCALE);
eraseOrder.push_back(idx); // FAIL_RATIO * 50%
}
for (i = 0; i < FAIL_RATIO*DATA_SCALE; i += 2)
{
int idx = idxrand(0, DATA_SCALE);
while (idx % 4 < 2)
idx = idxrand(0, DATA_SCALE);
findOrder.push_back(idx); // FAIL_RATIO * 50%
}
std::random_shuffle(insertOrder.begin(), insertOrder.end()); // using built-in random generator
std::random_shuffle(eraseOrder.begin(), eraseOrder.end()); // using built-in random generator
std::random_shuffle(findOrder.begin(), findOrder.end()); // using built-in random generator
/* execute operations of insert(), erase() and find() for both std::map and nonstd::map */
{
Timer timer("insertion of std::map costs: ");
for (i = 0; i < DATA_SCALE * (1+FAIL_RATIO); ++i)
std_map.insert(std::pair<int, double>(keys[insertOrder[i]], values[insertOrder[i]]));
}
{
Timer timer("insertion of nonstd::map costs: ");
for (i = 0; i < DATA_SCALE * (1+FAIL_RATIO); ++i)
nonstd_map.insert(std::pair<int, double>(keys[insertOrder[i]], values[insertOrder[i]]));
}
{
Timer timer("erasure of std::map costs: ");
for (i = 0; i < DATA_SCALE/2 * (1+FAIL_RATIO); ++i)
std_map.erase(keys[eraseOrder[i]]);
}
{
Timer timer("erasure of nonstd::map costs: ");
for (i = 0; i < DATA_SCALE/2 * (1+FAIL_RATIO); ++i)
nonstd_map.erase(keys[eraseOrder[i]]);
}
{
Timer timer("finding of std::map costs: ");
int existCount = 0;
for (i = 0; i < DATA_SCALE/2 * (1+FAIL_RATIO); ++i)
if (std_map.find(keys[findOrder[i]]) != std_map.end())
++existCount;
cout << "std::map::find() exist elements' count: " << existCount << endl;
}
{
Timer timer("finding of nonstd::map costs: ");
int existCount = 0;
for (i = 0; i < DATA_SCALE/2 * (1+FAIL_RATIO); ++i)
if (nonstd_map.find(keys[findOrder[i]]) != nonstd_map.end())
++existCount;
cout << "nonstd::map::find() exist elements' count: " << existCount << endl;
}
std_map.clear();
nonstd_map.clear();
cout << "From comparsion, we can draw a conclusion that the performance of nonstd::map is slightly better than std::map." << endl;
return 0;
}
宏 FAIL_RATIO 用来控制 find 的时候有大致多少比例的元素已经被前面的 erase 操作给去除了,由于 erase 也会重复去除相同的元素,因此最终执行 find 时找到的元素与宏 FAIL_RATIO 设定的值的比例关系不是线性的,下面运行结果中 std::map find 操作找到的元素与 nonstd::map find 操作找到的元素数目相同,这证明了 AVL 树实现的正确性。
测试代码其中三次的运行结果如下:
通过对比发现,采用 AVL 树实现的 nonstd::map 性能居然要比标准库中的 std::map 性能在平均意义上还要稍好一些,这或许是因为 AVL 树的平衡性要优于红黑树的平衡性所致,真正原因不明。不过在代码生产时,没必要为了这么一点儿性能优化而采用 nonstd::map,采用 std::map 一来是因为标准库的实现是能确保没有 Bug 的实现,而且 API 丰富,二来是任何编译器、任何硬件平台都支持标准库,不用担心程序的可移植性,而且程序员都熟悉 STL,一看到 std::map 就知道你用这个数据结构大致是做什么了。